新刊『テクノ・リバタリアン 世界を変える唯一の思想』（文春新書）の「はじめに 世界を数学的に把握する者たち」を出版社の許可を得て掲載します。3月19日（火）発売ですが、一部の書店さんではすでに店頭に並んでいるようです。見かけたら手に取ってみてください（電子書籍とAudibleも同日発売です）。
******************************************************************************************
乗っていた飛行機が乱気流に巻き込まれ、思わず叫び声をあげたことはないだろうか。
このとき、隣に座っていた乗客が、「ちょっと計算してみたんですが、この飛行機が墜落する確率は0.001％以下で、無視してかまいませんよ」といったら、あなたは「世界を支配する秘密結社」のメンバーの一人にたまたま出会ったことになる。
秘密結社といっても、フリーメーソンやイルミナティ、ディープステイトのことではない。こんなとき、次の数式を頭に浮かべている者たちのことだ。
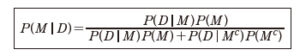これはベイズの定理で、ある状況が変化したとき、確率がどのように更新されるかを表わしている。
P は確率（Probability）の頭文字で、P（M｜D）は「飛行機がひどく揺れていると仮定した場合の墜落の確率」。それを計算するには「なにも起きていない段階で、飛行機が墜落する統計的確率（1000万分の1）」「墜落する前にひどい揺れが起きる確
率（これは間違いないので確率1＝100％）」「無事に着陸できるのにひどく揺れる確率（このような統計はすぐに手に入らないので、主観的に100分の1とする）」があればいい。これをベイズの数式にあてはめると、この飛行機が墜落する確率が10万分の1で、無事に着陸できる確率が99.999％であることがわかる(1)。
ベイズの定理がいっていることは、直観的にも説明できる。「統計的にものすごく低い確率でしか起こらないこと（飛行機の墜落）に、なんらかの要因（乱気流）が加わって確率がすこし上がったとしても、ヒドいこと（墜落）はやっぱりものすごく低い確率でしか起こらない」のだ。
ここまでは凡人でも理解できるだろうが、世の中にはこのようなとき、ごく自然にベイズの数式を呼び出し、それに数字をあてはめて計算し、どのように判断・行動するかを決めるひとがいる。それが「世界を数学的に把握する者たち」であり、本書の主人公である「テクノ・リバタリアン」だ。
リバタリアンは「自由原理主義者」のことで、道徳的・政治的価値のなかで自由をもっとも重要だと考える。そのなかできわめて高い論理・数学的知能をもつのがテクノ・リバタリアンで、現代におけるその代表がイーロン・マスクとピーター・ティールだ。
数学者のデイヴィッド・サンプターは、「成功、幸福、富などを与えてくれる10の数式（ベイズの定理もこのなかに含まれる）」を知る者たちを「ＴＥＮ」と呼び、その暗号を解き秘密の数式を自在に操ることで世界を支配しているという(2)。
その集団、いうなれば秘密結社は、実は何世紀も前から存在する。その秘密結社のメンバーたちは、代々自分たちの知識を後世に伝えてきた。そんな彼らは行政、金融、学界、そして最近ではテクノロジー企業の世界で実権を握り、一般人に紛れて過ごしつつも、私たちにこっそりと力強い助言を送り、時には私たちを陰で操ってさえいる。一般の人々が心から手に入れたいと望む秘密を見つけ出し、裕福で、満ち足りた、自信満々な人生を送っている。
ＴＥＮはデータを数学的にモデル化し、パターンを見つけてシグナル（必要な情報）とノイズ（不要なゴミ）を見分ける特殊な能力をもっている。だがこれは、世界の真実を知っているということではない。重要なのは、平均よりも精度の高い（現実をうまく説明する）モデルをもっていることだ。
カジノがビッグビジネスになるのは、自分たちが51％の確率で勝ち、客が49％の確率でしか勝てないビジネスモデルを構築したからだ。これなら、巨大な施設をつくって巨額の宣伝費を投じ、多くのギャンブラーを集めることで確実に儲けられる（実際には、カジノの客の勝率はもっと低いだろう）。
それに対して、ラスベガスとウォール街を攻略した数学者で「最強のハッカー」でもあるエドワード・ソープは、カジノの人気ゲームであるブラックジャックのバグを発見し、「カードカウンティング」によって51％以上の確率で勝てることを数学的に証明した（しかもそれを論文として公開した）(3)。その後、マサチューセッツ工科大学（ＭＩＴ）の学生たちがブラックジャックチームという「秘密結社」をつくり、カードカウンティングによって全米のカジノを荒らしまわり、巨額の富を手にすることになる(4)。
ＴＥＮの特殊な能力が成功に結びつくのは、わたしたちが生きているのが「知識社会」で、高い知能をもつ者に大きなアドバンテージが与えられるからだ。しかも、世界がよりゆたかに、より平和になるにしたがって、彼ら／彼女たちのパワーはますます強まっている。
戦争や内乱では武力が、貧しい社会では身分のような既得権が生き残るために必須だが、世界がゆたかで平和になればこれらは無用の長物になり、人種や国籍、出自、性別、性的指向などとは関係なく、一人ひとりの能力だけが公正に評価されるようになる。リベラルな社会の根幹をなすこの原理がメリトクラシーだ。
伝統的なムラ社会のしがらみが色濃く残る日本に比べて、「人工国家」であるアメリカは純化した知識社会で、その可能性に魅せられて世界じゅうからＴＥＮが引き寄せられてくる。こうして、シリコンバレーという唯一無二の特別な場所が生まれた。
日本では残念なことに、いまだに「思想」というと孔子や仏陀やプラトン、カントやマルクス、あるいは1980年代に流行したポストモダンのフランス思想のことだと思われているが、科学とテクノロジーの水準が指数関数的（エクスポネンシャル）に高度化したことで、これらはすべて過去の遺物になった（進化論を無視して人間や社会を語ることになんの意味があるのか）。
その結果、いまや世界を変える思想はリバタリアニズムだけになっている。このように言い切れるのは、Google、Amazon、Meta（Facebook）などプラットフォーマーの創業者、チャットＧＰＴなどのＡＩ（人工知能）や、ビットコインなどで使われるブロックチェーンの開発者がみなテクノ・リバタリアンだからだ。
そんな特殊能力をもつ「ミュータント」たちは、わたしたちをどのような世界に導いていくのか？ 本書ではこの問いを考えてみたい。
なぜなら、未来について語るのに、これ以外に真剣に考えるべきことなど存在しないからだ。
(1) ベイズの定理のうち、分子のP（M）はなにも起きていないときに墜落する統計的確率、P（D｜M）は飛行機がこれから墜落すると仮定した場合にひどく揺れる確率で、両者を掛け合わせることで2つの事象が両方とも成り立つ確率が求められる。分母はこれに補集合を加えたもので、起こりうるすべてのケースの和を表わす。PMc）は飛行機が墜落しない統計的確率、P（D｜Mc）は墜落しないのにひどく揺れる確率。
(2) デイヴィッド・サンプター『世界を支配する人々だけが知っている10の方程式 成功と権力を手にするための数学講座』千葉敏生訳／光文社
(3) エドワード・Ｏ・ソープ『天才数学者、ラスベガスとウォール街を制す 偶然を支配した男のギャンブルと投資の戦略』望月衛訳、ダイヤモンド社
(4) ベン・メズリック『ラス・ヴェガスをブッつぶせ！』真崎義博訳、アスペクト
禁・無断転載